zurück  ·   eMail an Autor  ·   Matheseitenüberblick

Der Schwerpunkt des Dreiecks

Auf dieser Seite wird schrittweise erklärt, warum der Schwerpunkt des Dreiecks im Schnittpunkt der Seitenhalbierenden liegt und warum er jede der Seitenhalbierenden in zwei Abschnitte trennt, von denen der größere doppelt so lang ist wie der kleinere.

Um alles nachvollziehen zu können, braucht man Kenntnisse der Berechnung von Dreiecksflächen (A=½·g·h), muß die Kongruenzsätze bei Dreiecken und die Strahlensätze kennen und schon mal was vom Lösen von Gleichungssystemen (speziell Addition von Gleichungen) gehört haben.

Was ist ein Schwerpunkt?

Unter dem Schwerpunkt versteht man den Punkt, der sozusagen der Mittelwert der "Masseverteilung" eines Körpers oder der "Flächenverteilung" einer Fläche ist. Wenn du mit einem Stuhl so kippelst, daß der Schwerpunkt von Stuhl und dir zusammen hinter den Hinterbeinen liegt, kippt alles nach hinten. (Deswegen beugt man sich beim Kippeln nach vorne, denn das verlagert den Schwerpunkt soweit nach vorne, daß er über den Hinterbeinen liegt. So bleibt man im Gleichgewicht...)
Ein ausgeschnittenes Dreieck muß man genau auf seinem Schwerpunkt auf eine Bleistiftspitze legt, nur so bleibt es genau in der Schwebe liegen, sonst kippt es und fällt runter. Es kann seinen Schwerpunkt ja schließlich nicht von selbst verlagern.

Wo liegt dieser Schwerpunkt?

Fangen wir mal von vorne an und überlegen zunächst, wie man ein Dreieck durch eine Gerade in zwei Teile teilt, die nicht nur "gleich schwer" sind, also den gleichen Flächeninhalt besitzen. Weil weiter von der Achse entfernte Flächenteile infolge des Hebelgesetzes proportional zum Abstand von der Achse "schwerer wiegen", reicht diese Flächengleichheit nicht aus. Wir werden jedoch sehen, daß die flächengleiche Teilung auch zu einer Teilung führt, bei der sich in jedem Abstand von der Achse auf beiden Seiten jeweils gleiche Flächenteile befinden.
 

Wie teilt man ein Dreieck in zwei Teile mit der gleichen Fläche?

Viele denken, das funktioniere mit Winkelhalbierenden, also mit den Geraden, die durch einen der Eckpunkte gehen und den Innenwinkel des Dreiecks genau halbieren. In der Abbildung rechts ist das Dreieck durch eine seiner Winkelhalbierenden in zwei Teile getrennt.

An sich sieht man schon an der ersten Abbildung, daß die Flächen der Teildreiecke nicht gleichgroß sind; deutlich wird es, wenn man das untere Teildreieck an der Winkelhalbierenden in das obere spiegelt. Schnell stellt man fest, daß das obere (natürlich) nicht vollständig abgedeckt wird und daher größer sein muß als das untere.

(Wie müßte eigentlich das Dreieck beschaffen sein, daß beide Teile bei der Spiegelung eines Teiles an der Winkelhalbierenden genau aufeinander fallen?)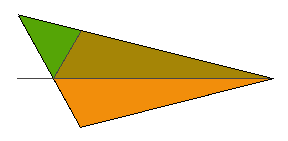

Übrigens besitzen ja beide Teildreiecke in der Winkelhalbierenden eine gemeinsame Seite. Wenn man jeweils die Höhen auf diese Seite konstruiert, so sieht man, daß die Höhe des oberen Dreiecks (h3) länger ist als die des unteren (h1), denn h3 > h2 und h2 = h1.

Bei gleicher Grundseite, aber unterschiedlichen Höhen müssen auch die Flächeninhalte unterschiedlich sein.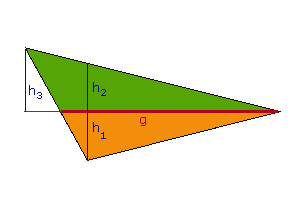

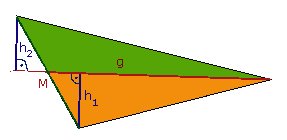
Anders verhält es sich, wenn man das Dreieck durch eine Seitenhalbierende teilt, also eine Gerade durch einen Eckpunkt und die gegenüberliegende Seitenmitte. An der Abbildung, der dasselbe Dreieck zugrundeliegt, erkennt man bereits, daß diese Gerade so links nach oben gedreht ist, daß die Fläche oben kleiner als vorher ist und unten größer. Doch stimmen sie jetzt überein?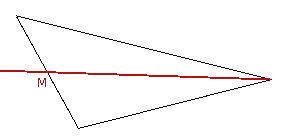

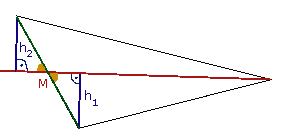
Wir konstruieren wieder die beiden Höhen und betrachten die beiden kleinen Dreiecke, welche links entstanden sind. Sie besitzen beide einen rechten Winkel, denn die Höhen stehen definitionsgemäß senkrecht auf der Grundseite. Die dem rechten Winkel jeweils gegenüberliegenden Seiten sind gleichgroß, denn es sind jeweils gleiche Hälften der großen Dreiecksseite. Außerdem sind die farblich markierten Winkel gleich, denn es sind Scheitelwinkel. Damit sind die beiden kleinen Dreiecke kongruent (Kongruenzsatz SWW). Infolgedessen müssen sie in allen entsprechenden Größen gleich sein, insbesondere muß gelten: h1 = h2.

Wenn aber h1 = h2, dann ist auch ½·g·h1 = ½·g·h2, und damit sind die beiden Teildreiecke ober- und unterhalb der Seitenhalbierende flächengleich.

Die Seitenhalbierende teilt das Dreieck in zwei Dreiecke mit gleicher Grundseite und gleicher Höhe. Damit sind sie nicht nur flächengleich, sondern die Teildreiecke können auch durch eine Scherung parallel zur Achse in eine achsensymmetrische Form überführt werden, die sicherlich auch bei Beachtung der Hebelgesetze auf der Symmetrieachse balanciert werden kann.

Diese Scherung parallel zur Achse verändert für keinen Punkt des gescherten Dreiecks den Abstand zur Achse, d.h. zur Seitenhalbierenden. Also ist auch das urspüngliche Dreieck zur Seitenhalbierenden auf beiden Seiten "gleich schwer".

Man kann folglich jedes Dreieck auf der Kante eines Lineals balancieren, wenn man es genau mit einer seiner Seitenhalbierenden auf die Linealkante legt. Probiere es aus!
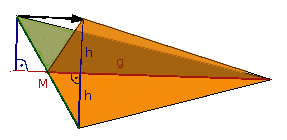
Balancieren des Dreiecks auf einer Bleistiftspitze

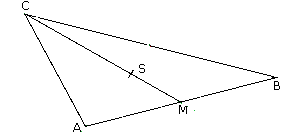
Wenn eine Seitenhalbierende das Dreieck in zwei flächengleiche (und damit "gleichschwere") Teile trennt, so muß der Punkt, auf dem es genau ausbalanciert werden kann, auf dieser Strecke liegen. Aber wo genau?

Um das herauszufinden, teilen wir das Dreieck einmal durch eine der beiden anderen Seitenhalbierenden. Auch auf dieser Linie kann das Dreieck balanciert werden, und der Schwerpunkt muß auch auf dieser Linie liegen.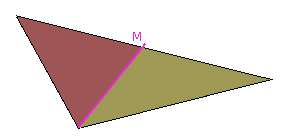

Jetzt ist es klar: Wenn der Schwerpunkt auf jeder einzelnen Seitenhalbierenden liegen muß, so liegt er genau da, wo sich beide schneiden, denn nur dort kann er auf beiden gleichzeitig liegen!

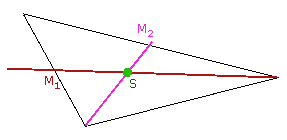Wunderbarerweise (und logischerweise) geht auch die dritte Seitenhalbierende durch diesen Punkt.

Der Schwerpunkt des Dreiecks ist der Schnittpunkt der drei Seitenhalbierenden.

Zeichne ein Dreieck und konstruiere die Seitenhalbierenden und damit den Schwerpunkt. Nun miß einmal die Teilstreckenlängen jeder Seitenhalbierenden vom Schwerpunkt zum Eckpunkt und vom Schwerpunkt zur Seitenmitte. Es fällt Dir sicherlich etwas auf!

Der Schwerpunkt teilt die Seitenhalbierenden in Abschnitte mit dem Längenverhältnis 1:2

Um die beiden folgenden Beweise zu verstehen, muß man die Strahlensätze kennen und (nur beim 1. Beweis) wissen, wie man Gleichungen voneinander subtrahiert.

1. Beweis

Durch die drei Seitenhalbierenden wird das Dreieck in sechs Teildreiecke geteilt. Je drei davon besitzen zusammen den selben Flächeninhalt, denn die Seitenhalbierenden teilen ja das Dreieck in zwei flächengleiche Teile:

A1 + A2 + A3 = A4 + A5 + A6
A2 + A3 + A4 = A5 + A6 + A1
A3 + A4 + A5 = A6 + A1 + A2

Subtrahiert man die zweite Gleichung von der ersten, so ergibt sich:

A1 - A4 = A4 - A1

Daraus folgt, daß A1 = A4.

Analog kann man die dritte von der ersten Gleichung subtrahieren sowie die dritte von der zweiten und erhält so insgesamt, daß die Flächeninhalte gegenüberliegender Dreiecke untereinander jeweils gleich sind.

Die jeweils benachbarten Dreiecke A2|A3, A4|A5 und A1|A6 besitzen ebenfalls paarweise den selben Flächeninhalt, da sie jeweils gleiche Grundseiten haben (die Hälfte einer großen Dreiecksseite) und identische Höhen.

Damit besitzen alle sechs kleinen Dreiecke denselben Flächeninhalt, denn A1 = A4 = A5 = A2 = A3 = A6

Wir betrachten die vierte und die sechste Dreiecksfläche. Die Höhen dieser Dreiecke sind parallel, da sie beide senkrecht auf der Seitenhalbierenden MB stehen. Damit entsteht eine Strahlensatzfigur mit dem Scheitel B.

Weil P die Strecke BC halbiert, ist |BC|:|BP| = 2:1.

Dann gilt nach dem 2. Strahlensatz auch h6:h4 = 2:1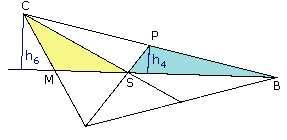

Die Dreiecke besitzen, wie wir oben gesehen haben, die selbe Fläche. Wenn aber die Höhe des linken doppelt so groß ist wie die des rechten, muß seine Grundseite halb so groß sein! Das bedeutet: |BS|:|MS| = 2, und damit teilt der Schwerpunkt S die Seitenhalbierende MB in zwei Abschnitte mit dem Längenverhältnis 2:1.

Analog kann man je zwei Teildreicke betrachten, die an den anderen Seitenhalbierenden anliegen und kommt zu analogen Ergebnissen für die Lage von S auf diesen Strecken.

 

2. Beweis

Wir zeichnen die Hilfsstrecke MaMc in das Dreieck ein.
Weil Ma und Mc jeweils die Mittelpunkte von CB bzw. AB sind, gilt |AB|:|McB| = 2:1 und |CB|:|MaB| = 2:1. Damit sind die beiden Strecken MaMc und AC parallel, und wir haben eine Strahlensatzfigur mit B als Scheitelpunkt.

Wir leiten daraus sofort ab, daß |AC|:|MaMc| = 2:1.

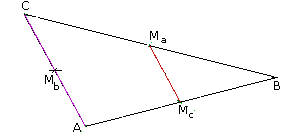Wir betrachten nun die beiden Seitenhalbierenden AMa und CMc, die mit dem Schwerpunkt S als Scheitel und den beiden Parallelen AC und MaMc ebenfalls eine Strahlensatzfigur bilden. (Die Parallelen liegen hierbei auf verschiedenen Seiten des Scheitelpunktes.)

Wegen |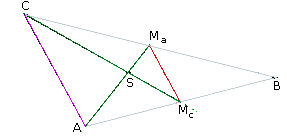AC|:|MaMc| = 2:1 muß gelten: |AS|:|SMa| = 2:1 und für die andere Seitenhalbierende |CS|:|SMc| = 2:1.

 

3. Beweis

Mit linearer Algebra und analytischer Geometrie läßt sich sowohl der Satz als auch die nachfolgende Regel über die Koordinaten des Schwerpunktes recht einfach zeigen. Siehe unten.

Die Koordinaten des Schwerpunktes

Das Dreieck ABC sei mit den Koordinaten seiner Eckpunkte gegeben. (xA|yA) seien die Koordinaten von A, (xB|yB) die von B und (xC|yC) die von C.

Die Koordinaten des Mittelpunkts von AB berechnen sich durch das arithmetische Mittel der Koordinaten von A und B: M = ( (xA+xB)/2 | (yA+yB)/2 ).

Der Schwerpunkt S liegt so auf der Strecke MC, daß |CS|:|SM| = 2 (siehe oben). Dies gilt wieder auch für die einzelnen Koordinaten, so daß
(xS-xC) / (xM-xS) = 2 und (yS-yC) / (yM-yS) = 2.

Die erste Gleichung wird nach xS aufgelöst:

(xS - xC) / (xM - xS) = 2      | · (xM - xS)
xS - xC = 2·(xM - xS) | Ausmultiplizieren
xS - xC = 2xM - 2xS | + 2xS + xC
3xS = 2xM + xC | Nun wird xM ersetzt durch (xA+xB)/2
3xS = 2·(xA + xB)/2 + xC | 2 kürzen
3xS = xA + xB + xC | :3
xS = (xA + xB + xC)/3
Analog gilt für yS:
yS = (yA + yB + yC)/3

Die Koordinaten des Schwerpunkts sind das arithmetische Mittel der Koordinaten der Eckpunkte.

 

3. Beweis
Die Seitenhalbierende zu a liegt auf der Geraden sa durch A und die Mitte von a. Der Stützvektor der Geradengleichung sei A, der Richtungsvektor die Differenz aus 0Ma und 0A. So ergibt sich für λ=1 der Ortsvektor von Ma. Die Vermutung ist, daß man für λ=2/3 den Ortsvektor von S erhält.      
Die Koordinaten der Mitte von a sind die arithmetischen Mittelwerte der jeweiligen Koordinaten von B und C: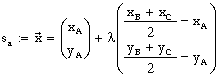
Die Komponenten des Richtungsvektors werden auf einen Bruchstrich geschrieben: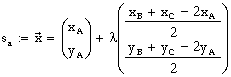
Analog erhält man die Geradengleichung für sb: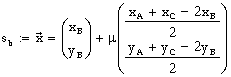
λ=1 und μ=1 ergeben jeweils die Ortsvektoren der Seitenmitten von a bzw. b; nach unserer Vermutung müßten dann λ=μ=2/3 jeweils S ergeben. Es gilt jedenfalls folgendes: Ergibt sich mit λ=μ=2/3 jeweils der selbe Punkt, muß dieser auch der Schnittpunkt der Geraden sa und sb, d.h. der Seitenhalbierenden sein, und den Punkt nennt man ja S.
 
Tatsächlich ergibt sich sowohl bei sa mit λ=2/3 als auch bei sb mit μ=2/3 der selbe Ortsvektor.
Und es bestätigt sich auch gleich, daß die Komponenten dieses Ortsvektors, OS, die arithmetischen Mittelwerte der Komponenten der Ortsvektoren der Eckpunkte sind:
 

 

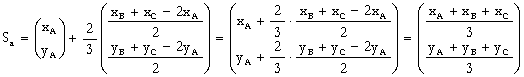zurück
© Arndt Brünner
Dreiecksberechnung
Dreiecksrechner (Vorgabe der Seitenhalbierenden möglich)
Konstruktion eines Dreiecks aus den Seitenhalbierenden
Matheseitenüberblick
Version: 11. 3. 2013