Numerische Lösung nichtlinearer Gleichungssysteme

Dieses Javascript sucht nach numerischen Lösungen beliebiger Gleichungssysteme.
Geben Sie im oberen Feld zeilenweise die Gleichungen ein. Der Erfolg des verwendeten Algorithmus*⁾ hängt eklatant von der Güte der Anfangsnäherungen ab. Im mittleren Feld können optional Startwerte für Variablen festgelegt werden. Beispiel: x=-1,5 y=4 z=[2...3,5]. Im Beispiel wird der Startwert für z im Intervall von 2 bis 3,5 zufällig gewählt. Wenn für eine vorkommende Variable kein Startwert angegeben wird, so wählt das Script ihn zufällig zwischen -10 und 10. Wird bei zufälligen Startwerten keine Lösung gefunden, so lassen Sie mehrfach suchen oder erhöhen den Wert bei max. Anzahl der Durchläufe. An Variablennamen sind alle Buchstaben möglich. Klein- und Großschreibung wird nicht unterschieden.

Unterstützte Funktionen, Operatoren und Konstanten:
+ - * / ^ ( ) pi e_ phi sqr sqrt log exp abs int sin asin cos acos tan atan atn cot acot sec asec csc acsc sinh asinh cosh acosh tanh atanh atnh coth acoth sech asech csch acsch

Der verwendete Algorithmus
 
...ist eine Erweiterung des Newtonverfahrens zum Approximieren von Nullstellen auf mehrere Dimensionen. Um Lösungen einer Gleichung als Nullstelle zu gewinnen, muß die Gleichung LinkeSeite = RechteSeite in der Form Term = 0 vorliegen. Das kann leicht bewerkstelligt werden, indem man schreibt: LinkeSeite - (RechteSeite) = 0. Lösungen dieser Gleichung sind dann die Nullstellen der Funktion f := LinkeSeite - (RechteSeite)

Auch die Proben im obigen Skript werden anhand dieser Funktionen durchgeführt. Eine Lösung liegt dann vor, wenn alle f an der gefundenen Stelle 0 werden.

Bei eindimensionalen Funktionen ℜ→ℜ gewinnt man ausgehend von einer günstigen Startnäherung für x bessere Näherungen durch die Rekursion x_i+1 = x_i - f(x)/f'(x) = x_i - f(x)·(f'(x))^-1, wobei f'(x) die erste Ableitung von f(x) ist.

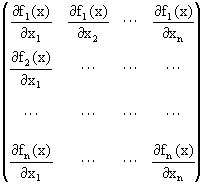
Im ℜⁿ tritt anstelle der Ableitung die Jacobimatrix J_f(x)

bzw. an die Stelle von (f'(x))^-1 die inverse Jacobimatrix.

Die Nullstellen eines dreidimensionalen Gleichungssystems mit den Variablen x, y und z sowie den Funktionen f₁(x,y,z), f₂(x,y,z) und f₃(x,y,z) werden durch folgende Rekursionen angenähert:

     xi+1 = xi - j1,1·f1(x,y,z) - j1,2·f2(x,y,z)- j1,3·f3(x,y,z) 
     yi+1 = yi - j2,1·f1(x,y,z) - j2,2·f2(x,y,z)- j2,3·f3(x,y,z) 
     zi+1 = zi - j3,1·f1(x,y,z) - j3,2·f2(x,y,z)- j3,3·f3(x,y,z)

wobei j_2,3 das Element in der 2. Zeile und der 3. Spalte der inversen Jacobimatrix ist.

Die partiellen Ableitungen in der Jacobimatrix werden im Skript durch Differenzenquotienten mit sehr kleinem d approximiert: ∂f/∂x ≈ (f(x+d)-f(x))/d.

Die inverse Jacobimatrix wird gefunden über den Gauß-Algorithmus durch Umformen der Jacobimatrix in die Einheitsmatrix und paralleles Umformen einer Einheitsmatrix mit denselben Transformationen. Näheres zu diesem Verfahren findet sich →hier.

© Arndt Brünner, 9. 8. 2003 — Version: 24. 10. 2003
    eMail
→ lineare Gleichungssysteme berechnen
→ Gleichungen mit einer Variablen approximieren
→ Inverse Matrizen berechnen