|
In der nebenstehenden Strahlensatzfigur sind jeweils einige Strecken gegeben. Berechne die gesuchten Strecken |
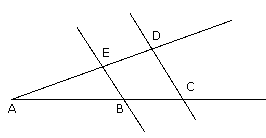
|
geg.: |AB| = 5cm; |BC| = 2cm; |ED| = 2,5cm
ges.: |AE|1. Strahlensatz: |AE| |AD| —————— = —————— |AB| |AC| Um zu zeigen, daß man auch mit den Einheiten rechnen kann und am Schluß die richtige Einheit herauskommt, rechne ich die erste Aufgabe mal mit Einheiten durch. Bitte achtet drauf, gegebenenfalls immer erst auf gleiche Einheiten umzurechnen! Bei den Teilaufgaben c) und d) ist das erforderlich. x x + 2,5cm ————— = ——————————— 5cm 5cm + 2cm x x + 2,5cm ————— = ——————————— | · 5cm 5cm 7cm 5cm(x + 2,5cm) x = ———————————————— 7cm 5cm·x + 12,5cm² x = ———————————————— | · 7 cm 7cm 7cm·x = 5cm·x + 12,5cm² | - 5cm·x 2cm·x = 12,5cm² | : 2cm x = 6,25cmgeg.:|AC| = 2,5km; |CD| = 3,1km; |BE| = 2,9km
ges.: |BC|2. Strahlensatz: |AC| |AB| —————— = —————— |CD| |BE| Es gibt zwei Möglichkeiten. Bei der ersten rechnet man nach dieser Formel zunächst |AB| direkt aus und schließt dann auf |BC| = |AC| - |AB|. Bei der zweiten setzt man für |AB| in die obige Formel |AC| - |BC| ein. Erste Möglichkeit: 2,5 |AB| ————— = ————— | ·2,9 3,1 2,9 7,25 ————— = |AB| = 2,3387...km 3,1 |BC| = |AC| - |AB| = 2,5km - 2,3387km = 0,16129km = 161,29m Zweite Möglichkeit: 2,5 |AC| - |BC| ————— = ————————————— 3,1 2,9 2,5 2,5 - |BC| ————— = ———————————— | · 2,9 3,1 2,9 7,25 ————— = 2,5 - |BC| | - 2,5 3,1 -0,16129 = -|BC| | · (-1) 0,16129 = |BC| = 169,29m
-
geg.: |AD| = 76cm; |AE| = 56cm; |BC| = 1,5m
ges.: |AB|Hier ist eine Einheitenumrechnung erforderlich! Ich rechne mit cm. 1. Strahlensatz |AB| |AC| —————— = —————— |AE| |AD| |AB| |AB| + |BC| —————— = ———————————— |AE| |AD| |AB| |AB| + 150 —————— = ———————————— | · 56 · 76 56 76 76·|AB| = 56·(|AB| + 150) 76·|AB| = 56·|AB| + 8400 | - 56·|AB| 20·|AB| = 8400 | : 20 |AB| = 420 |AB| = 4,2m geg.: |BE| = 23mm; |CD| = 3,1cm; |BC| = 12mm
ges.: |AB|Ich rechne mit mm, d.h. |CD| = 31mm 2. Strahlensatz: |AB| |AC| —————— = —————— |BE| |CD| |AB| |AB| + |BC| —————— = ————————————— |BE| |CD| |AB| |AB| + 12 —————— = ——————————— | · 31 · 23 23 31 31·|AB| = 23·(|AB| + 12) 31·|AB| = 23·|AB| + 276 | - 23·|AB| 8·|AB| = 276 |AB| = 34,5mm = 3,45cm
Die Höhe eines Turmes soll berechnet werden, dessen Schatten zur gleichen Zeit 18,45m lang ist, wo ein Stab der Länge 2m einen Schatten von 2,68m wirft.
Da das Sonnenlicht zur gleichen Zeit mit dem selben Winkel einfällt, sind die Dreiecke,
die die Schattenlinien auf dem Boden, der Stab bzw. der Turm und die Strecken von Stab-
bzw. Turmspitze zur Schattenspitze bilden, ähnlich, wenn Stab und Turm senkrecht stehen.
Ähnlich bedeutet, sie haben gleiche Streckenverhältnisse, und die gesuchte Turmhöhe h
verhält sich zur Turmschattenlänge t wie die Stablänge l zur Stabschattenlänge s:
h l
——— = ———
t s
h 2
——————— = —————— | · 18,45
18,45 2,68
36,9
h = —————— ~ 13,769
2,68
Die Turmhöhe beträgt ca. 13,78m.
Berechne die Entfernung der Türme voneinander. Die angegebenen Strecken wurden gemessen, die Strecken AC und BT2 sind parallel.
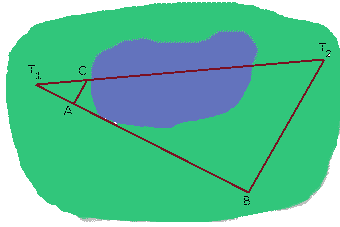 |
|T1A| = 100m |AB| = 350m |BT2| = 420m |AC| = 75m |
Gesucht ist x = |T1T2|
Hier schüttelt der Mathematiker den Kopf über den Vermessungsingenieur; vielleicht
haben sich die beiden mißverstanden oder vergessen miteinander zu reden, oder sie
verstehen beide nicht viel von den Strahlensätzen:
Irgendwas hat jedenfalls nichts geklappt!
Um x berechnen zu können, müßte nämlich in jedem Fall |T1C| bekannt sein.
Diese Strecke fehlt aber in der Messung.
Berechnungsansatz mit 1. Strahlensatz: |T1T2| |T1B| —————— = ————— |T1C| |T1A| Berechnungsansatz mit 2. Strahlensatz: |T1T2| |T1C| —————— = ————— |T2B| |AC|
Man kann mit dem 2. Strahlensatz aber überprüfen, ob die Messungen überhaupt stimmen!
|T1B| |T1A| —————— = ————— |T2B| |AC| 450 100 ————— = ————— 420 75 1,07142857142857... = 1,33333333333333... ??? O weia, dabei kommt es raus: Der Ingenieur wird wohl Ärger bekommen!
Nach dieser kleinen Gemeinheit zurück zu echter Mathematik
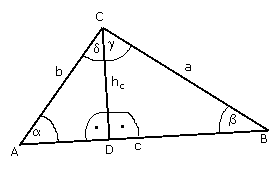 |
Das Dreieck ABC ist rechtwinklig mit c als Hypotenuse. Es wird durch die
Höhe hc in zwei kleinere Dreiecke (ADC und DBC) unterteilt. |
Die Ähnlichkeit zeigt man, indem man nachweist, daß die Dreiecke in ihren drei Winkeln gleich sind. Dazu reicht es schon, die Gleichheit von je zwei Winkeln nachzuweisen, denn durch die konstante Winkelsumme von 180° für alle Dreiecke ist dann auch der jeweils dritte Winkel gleich.
Da bei C ein rechter Winkel liegt, gilt:
Man kann den Winkel β berechnen, denn im Dreieck DBC gilt
Da nun γ + δ = 90° ist und
γ + δ = 90°
90° - β + δ = 90° | - 90°
- β + δ = 0 | + β
β = δ
Offensichtlich sind die beiden Innendreiecke ähnlich, denn sie haben beide einen rechten
Winkel bei D und außerdem mit
Vielleicht fällt es jemandem auf: Die beiden kleinen Dreiecke sind sich nicht nur einander ähnlich, sondern zur Ähnlichkeitsgesellschaft gesellt sich auch das große Dreieck ABC selbst, denn auch das ist ja rechtwinklig und hat mit α und β je einen Winkel mit den kleinen Dreiecken direkt gemeinsam.
Wenn man das sieht, kann man die Ähnlichkeit noch schneller zeigen.
Betrachte das große Dreieck ABC und das linke kleine Dreieck ADC. In beiden beträgt die
Winkelsumme 180°, beide besitzen einen rechten Winkel und beide teilen sich α.
Die dritten Winkel müssen daher gleich sein:
Analog beweist man
Unterteile eine Strecke der Länge 12cm ohne zu rechnen (Projektionssatz) je in zwei Teile mit dem Streckenverhältnis
a) 5:12 b) 7:3 c) 1:7
Zeichne die 12cm-Strecke AB. Zeichne dann bei a) eine Strecke AC, die 17cm lang ist,
mit AB einen leicht spitzen Winkel bildet und nach jedem Zentimeter eine Markierung besitzt.
Zeichne die Strecke CB. Zeichne dann Parallelen zu CB durch jede Markierung auf AC.
Die Parallelen zerschneiden AB in
Bei b) zeichne AC 10cm lang, bei c) 8cm.
Version: 16. 5. 2002
© Arndt Brünner
Matheseiten-Übersicht
Mathe-Forum
zurück